Sportsbook odds are not “true” probabilities. They include vig (juice) the sportsbook’s built-in margin. To evaluate whether a bet is actually good value, you need to calculate the true odds (also called fair odds) by removing that margin.
This article shows the exact process step by step, using simple formulas you can paste anywhere.
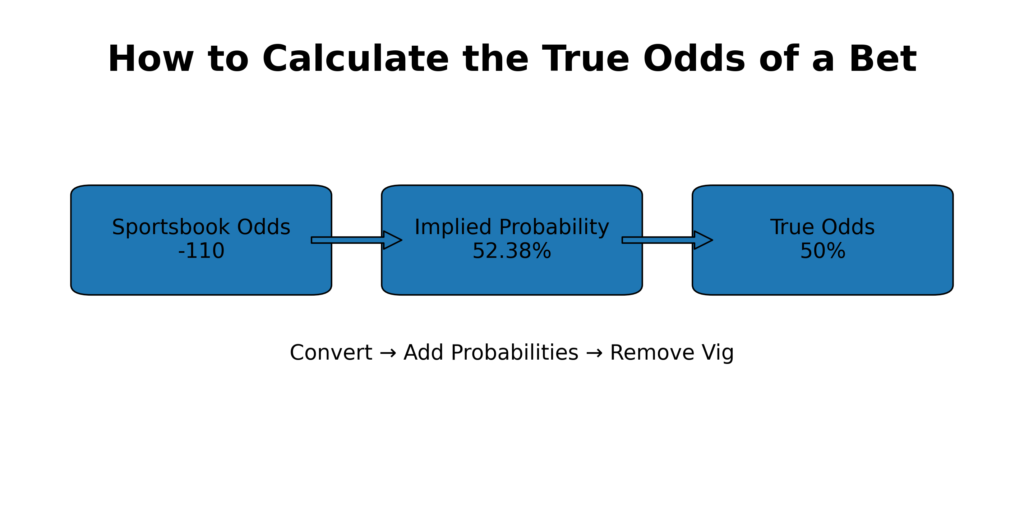
What Are “True Odds”?
True odds represent the fair probability of an outcome without the sportsbook’s margin.
Example:
- Sportsbook prices both sides at -110 / -110
- That looks like a 50/50 bet, but it’s not
- The extra cost (-110 instead of -100) is the vig
To find true odds, you:
- Convert odds to implied probability
- Add probabilities to find the margin (overround)
- Normalize probabilities (remove vig)
- Convert back to fair odds
Step 1: Convert Odds to Implied Probability
A) American odds (negative) e.g., -110
Implied Probability = ABS(odds) / (ABS(odds) + 100)
Example for -110:
Implied Probability = 110 / (110 + 100)
= 110 / 210
= 0.5238 (52.38%)
B) American odds (positive) e.g., +150
Implied Probability = 100 / (odds + 100)
Example for +150:
Implied Probability = 100 / (150 + 100)
= 100 / 250
= 0.40 (40%)
Step 2: Add the Implied Probabilities (Find the Overround)
Add the implied probabilities of all possible outcomes.
Example: -110 / -110
Side A: 52.38%
Side B: 52.38%
Total = 52.38% + 52.38% = 104.76%
That extra amount above 100% is the sportsbook’s margin.
Overround (vig) = 104.76% – 100% = 4.76%
Step 3: Remove the Vig (Normalize Probabilities)
To remove the vig, divide each implied probability by the total implied probability.
True Probability = Implied Probability / Total Implied Probability
Example:
Total implied probability = 104.76% (or 1.0476)
Side A true probability:
0.5238 / 1.0476 = 0.50 (50%)
Side B true probability:
0.5238 / 1.0476 = 0.50 (50%)
So the fair probabilities are 50% / 50%.
Step 4: Convert True Probability Back to Odds
Once you have true probability, convert it back to odds.
A) Convert probability to American odds (if probability > 50%)
American odds = – (P / (1 – P)) x 100
Example: P = 0.55
American odds = – (0.55 / 0.45) x 100
= -1.2222 x 100
= -122
So if the true probability is 55%, fair odds are about -122.
B) Convert probability to American odds (if probability < 50%)
American odds = ((1 – P) / P) x 100
Example: P = 0.40
American odds = (0.60 / 0.40) x 100
= 1.5 x 100
= +150
Full Worked Example (Uneven Moneyline)
Market:
- Team A: -150
- Team B: +130
Step 1: implied probabilities
Team A (-150):
150 / (150 + 100) = 150 / 250 = 0.60 (60%)
Team B (+130):
100 / (130 + 100) = 100 / 230 = 0.4348 (43.48%)
Step 2: add them
Total = 0.60 + 0.4348 = 1.0348 (103.48%)
Step 3: remove vig (normalize)
Team A true probability:
0.60 / 1.0348 = 0.580 (58.0%)
Team B true probability:
0.4348 / 1.0348 = 0.420 (42.0%)
Those are the fair market probabilities after removing the sportsbook margin.
Why Calculating True Odds Matters
1) It helps you identify value bets
Your edge exists only when your estimated probability is higher than the true market probability (after removing vig).
What Is Expected Value (EV) and Why It Matters in Betting
2) It helps you compare sportsbooks properly
Raw odds can be misleading. Removing vig lets you compare prices fairly across books.
What Is Line Shopping and Why It’s Important
3) It improves long-term evaluation
True odds help you judge whether you’re consistently beating market prices.
Why Beating the Closing Line Matters
Conclusion
Calculating true odds is a fundamental betting skill because it converts sportsbook prices into fair probabilities. Once you remove vig, you can evaluate bets accurately, compare lines across sportsbooks, and measure value correctly.
In sports betting, long-term profitability starts with understanding price and true odds are where price becomes clear.